![]()
cription-url="http://www.yinpinjie.com/file/upload/202208/03/192003201.png" src="http://www.yinpinjie.com/file/upload/202208/03/192003201.png" style="box-sizing: border-box !im
portant;overflow-wrap: break-word !im
portant;visibility: visible !im
portant;width: 677px !im
portant;" />

—— 本文最先刊登在SCA网站 ——在一个挤满咖啡爱好者的房间里要想引发一场激烈的争论,最好的方法之一就是问一个简单的问题:滴滤咖啡用什么形状的滤杯最好?SCOTT FROST博士、JEAN-XAVIER GUINARD教授和WILLIAM D. RISTENPART教授分享了与SCA和Breville公司合作进行的一个研究项目的早期成果。滴滤咖啡都需要一个滤杯,要么是锥形要么是平底扇形。锥形滤杯粉丝们称锥形滤杯提高流过咖啡粉床的流量,增加萃取均匀度,相应地改善口味。令人困惑的是喜欢平底扇形滤杯的人会说平底扇形滤杯也有同样的好处。支持一种观点或另一种观点的证据往往涉及个人的口味。到目前为止,对此争论缺少的是科学数据。2017年,SCA要求加州大学戴维斯咖啡中心(University of California Davis Coffee Center)开展研究,旨在更新传统滴滤咖啡萃取控制表( brewing co
ntrol chart)。这项研究正在进行中(取得了令人兴奋的初步结果)。我们也决定尝试着解决有关锥形滤杯和平底滤杯的争论。我们很幸运地与Breville Corporation合作,Breville Corporation滴滤机其特点是可以轻松地更换锥形滤杯和平底扇形滤杯。我们实验的思路是在保持所有其他冲煮变量不变(烘焙度、水温、流速等)的情况下评估滤杯形状对咖啡风味的影响。设计实验回答“哪种形状的滤杯更好?”你首先要回答这个问题:“二者有区别吗?”为了确定是否存在差异,我们首先使用了“辨别测试”,也称为“三角杯测”。在这个测试中,一名测试小组成员将得到三杯咖啡,其中两杯是相同的,另一杯是不同的。小组成员要找出不同的那杯咖啡。由于每个小组成员都有三分之一的机会仅凭运气就能猜对,所以我们需要33%以上的小组成员能正确地识别出那杯不同的咖啡。如果这个前提没有达成,那么就证明两个不同形状的滤杯没有任何实质的区别。我们招募了45名非专家小组成员来品尝在加州大学戴维斯咖啡中心感官实验室里滴滤好的咖啡。实验室分成小隔间将测试者隔离开,测试方式是盲测,室内设有红灯用来减少基于咖啡颜色深浅的预判偏差。在三角形测试中,我们使用了所谓的“2×2”阶乘设计,使用了两种形状的滤杯和两种不同的研磨度(中度和中细)。这是“析因设计”的一种方式(析因设计(factorial design)是实验设计的一种。指以多因素(两个或两个以上)为研究对象,探求各因素的主效应和因素间的交互效应)我们进行了六组不同的三角形杯测,测试所有可能的组合(滤杯形状+研磨度(表1))。另外单独一组测试是滤杯形状和烘焙度的组合(两种烘焙度:深,浅)。测试的重点是确定滤杯形状和研磨粗细的相互影响。实验中最具挑战性的一个问题是准备细节,因为三角杯测的后勤准备工作非常重要。例如,如果有两杯咖啡比第三杯咖啡温度高,那么小组测试成员只是在区别温差而不是味觉上的差别,所以我们必须制定出程序,在完全相同的温度下,提供不同的咖啡。同样,我们发现我们必须将“倒注水高度”规定好,因为我们的一些志愿者注水高度高于其他人,由此产生了咖啡表面泡沫的差异,测试者仅仅通过视觉观察就可以看出咖啡之间的不同之处。我们花了相当多的时间来研究这些细节,以确保实验的严谨性。计算结果我们的努力是值得的,因为我们获得了令人兴奋的(而且违反直觉的)结果,总结在表1中。关注第一行,我们看到,当比较锥形滤杯和平底扇形滤杯的形状时,都使用了中等研磨度,45名小组测试成员中有25人正确识别出了那杯不同的咖啡。(之前我们我们预计小组成员中有三分之一的人(15人)仅仅靠运气就能答对)。
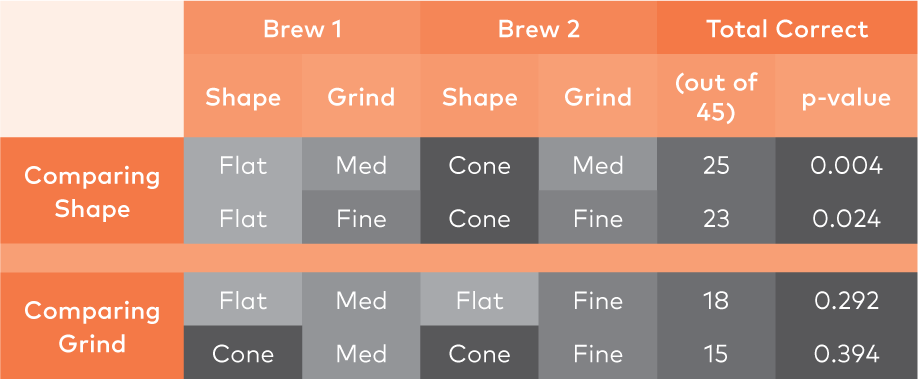
表1现在的问题重点是:这25人是不是靠运气猜对的。为了回答这个问题,我们使用了所谓的“二项概率分布”。二项概率分布伯努利试验设试验E只可能有两种结果:“A”和“非A”,则称试验E为伯努利试验例如抛硬币其结果可有两个若“A”表示得到正面则“非A”表示得到反面(如前文所述,在本次实验中,“硬币”正面朝上的概率为33%,即45人中有15人凭运气就可以猜出哪杯是不同的咖啡)将E独立的重复地进行n次,则称这一串重复的独立试验为n重伯努利试验二项分布亦称“伯努利分布”.设将一伯努利试验重复了n次,在这n次试验中成功次数x,x为随机变量,称为二次随机变量,其分布称为二项分布.假设每次成功的概率为p,则在n次试验中成功k次的概率为 p(x=k)=Cnk Pk(1-p)n-k (0≤k≤n)利用这个分布,我们能够计算出25位小组成员仅仅靠随机运气得到正确答案的概率或“p值”。这里的p值是0.004,这意味着如果我们重复实验1000次,25个小组成员在这1000个实验中只有4人可以正确找到那杯不同的咖啡。这个分布概率推断这不太可能!换句话说,这25人不是侥幸地找到那杯不同的咖啡,咖啡风味(从统计学角度看)上有显著的可察觉的差异。我们观察到一个类似的结果,对于使用锥形滤杯和平底扇形滤杯冲煮更细研磨度的咖啡,测试小组成员中有23人可以找出那杯不同的咖啡(p值为0.024)。因此,对于所有认为滤杯形状会影响咖啡口感的咖啡爱好者来说,我们的数据表明他们的这个论点是绝对成立的。然而,令人惊讶的是三角杯测也显示,这些非专家小组测试成员无法区分研磨度粗细(对风味影响)的差异。表1的第3行和第4行显示了同样形状滤杯但不同研磨度的三角杯测结果。使用平底扇形滤杯时,只有18名小组成员找出了不同的咖啡;而在使用锥形滤杯时也才有15人识别出不同的咖啡。这个概率非常低。我们的“中等研磨”的粒度为1065微米,而我们的“中细研磨”的粒度为799微米,大小相差25%。对于那些认为精确控制咖啡研磨大小的极端重要的咖啡爱好者来说,事实证明——至少对于滴滤咖啡来说——普通人分辨不出两者之间的区别(至少需要超过这个研磨度大小的范围)。上面描述的三角杯测显示出了明显的区别,但是它们没有说明区别是什么。为了解决这个问题,我们接下来进行了一系列详细的“感官描述”实验(sensory des
criptive experiments)。在这种类型的测试中,我们请训练有素的专家小组成员评估各种味道属性的强度,如“烟熏味”、“柑橘味”、“苦味”等。我们也邀请了表现最好的非专家小组成员(那些在三角杯测中表现最好的人)加入我们的专家小组。我们对他们进行了感官校正。然后,我们让他们评估来自8种不同设计组合(“2×2×2”阶乘设计:2种滤杯形状,2种研磨度,2种烘焙度)的26种不同的风味属性(flavor attributes)。专家小组盲测了了每种组合,并提供了26种风味属性的先后排名。12名专家小组成员,每个人品测26个风味属性,8个不同的组合,重复3次,得到12×26×8×3 = 7,488个个体数据点。不用说采集这么大的数据集很有挑战性。图2中提供了一个图像摘要,展示了所谓的“主成分分析”。这是一种先进的统计技术,用于获取大量数据集,并将其缩减为最有意义的“主成分”,以帮助确定小组中哪些人的感官最不相似或最相似。
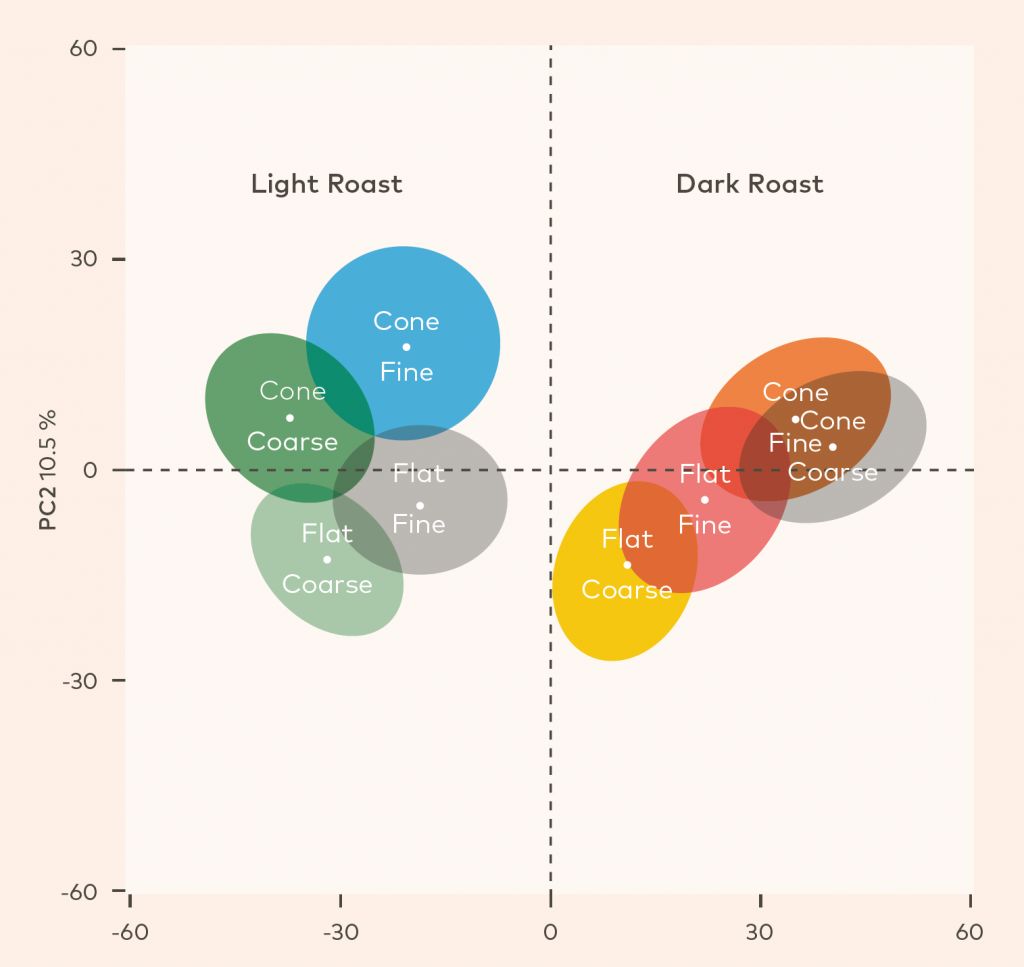
图2图2为主成分分析图,将最相似的统计结果分组在一起。从这里,我们可以看出最大的区别是浅烘焙和深烘焙之间的区别,而且滤杯的形状也对差异发生了实质作用。
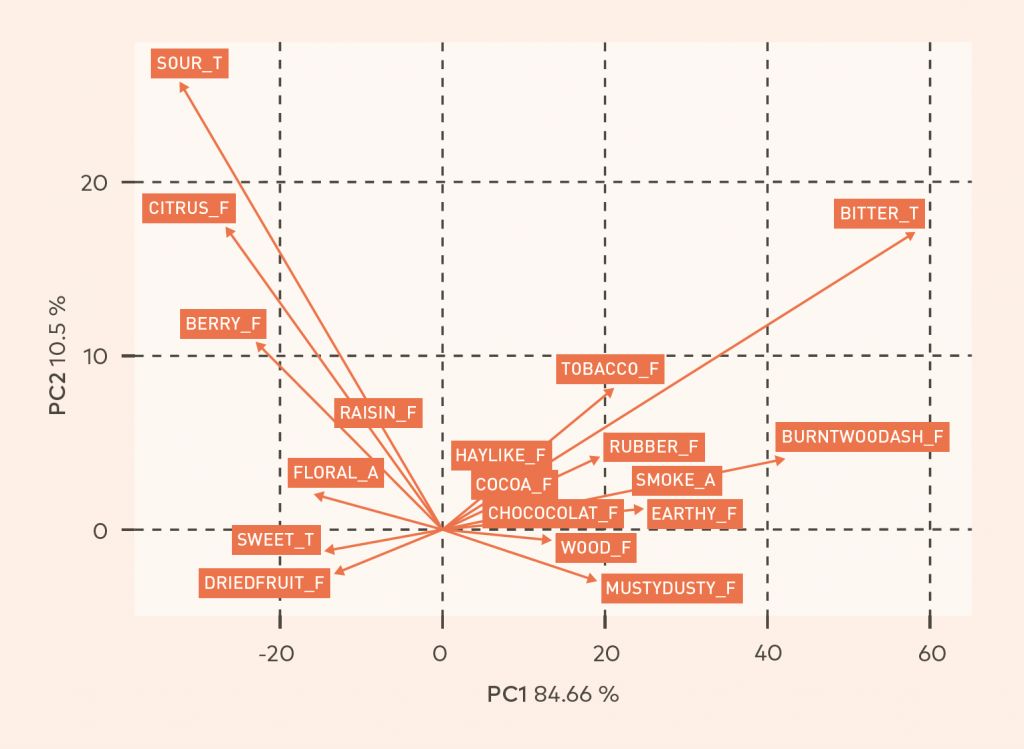
图3:概述了每个分组的风味属性。锥形滤杯的浅烘焙咖啡带有酸感,柑橘和浆果的味道;风味描述中有葡萄干、干果和甜美的花香。从上图中可以得到一些有用的信息。首先,不出意料的是,浅烘焙和深烘焙之间存在着很大的风味差异。更有趣的是,我们发现对于给定的烘焙度(例如,左边的浅烘焙)滤杯形状也产生了有意义的差异。平底滤杯有更多的干果、甜感和花香,而锥形滤杯则有更多的柑橘、浆果和酸感。同样的,滤杯的形状也影响了深烘焙,平底滤杯产生了更明显的巧克力、可可和木质口味,而锥形滤杯则产生了更强烈的苦味。哪个形状的滤杯最好?这是一个关键点,让我们重申一下:使用完全相同的咖啡,相同的水,相同的温度,相同的流量,我们能够通过改变滤杯形状(以一种非常明显的,统计上显著的方式)改变咖啡的风味。在证明了存在差异以及差异是什么之后,最后一个问题是“为什么存在差异?”滤杯的形状会影响液体流过咖啡粉床的方式,从而改变分子从固体(咖啡颗粒)中被萃取及进入液体的“质量传递”过程。这个过程的基本细节是复杂的;加州大学戴维斯咖啡中心(UC Davis Coffee Center)正在积极深入地研究这一点。对于:“哪种形状的滤杯是“最好的”?答案应该是:最适合你的口味的冲煮方式就是“最好的”,这取决于每个人的决定。(这个结论结论似乎一万年前,所有的人都知道)不过,至少,下次有人开始讨论平底滤杯和锥形滤杯的优缺时,您可以使用本文中的数据来阐明这场争论。全文完

看的懂的看不懂的,动动手指分享到朋友圈好东西,就是要分享!也欢迎留言!
 —— 本文最先刊登在SCA网站 ——在一个挤满咖啡爱好者的房间里要想引发一场激烈的争论,最好的方法之一就是问一个简单的问题:滴滤咖啡用什么形状的滤杯最好?SCOTT FROST博士、JEAN-XAVIER GUINARD教授和WILLIAM D. RISTENPART教授分享了与SCA和Breville公司合作进行的一个研究项目的早期成果。滴滤咖啡都需要一个滤杯,要么是锥形要么是平底扇形。锥形滤杯粉丝们称锥形滤杯提高流过咖啡粉床的流量,增加萃取均匀度,相应地改善口味。令人困惑的是喜欢平底扇形滤杯的人会说平底扇形滤杯也有同样的好处。支持一种观点或另一种观点的证据往往涉及个人的口味。到目前为止,对此争论缺少的是科学数据。2017年,SCA要求加州大学戴维斯咖啡中心(University of California Davis Coffee Center)开展研究,旨在更新传统滴滤咖啡萃取控制表( brewing control chart)。这项研究正在进行中(取得了令人兴奋的初步结果)。我们也决定尝试着解决有关锥形滤杯和平底滤杯的争论。我们很幸运地与Breville Corporation合作,Breville Corporation滴滤机其特点是可以轻松地更换锥形滤杯和平底扇形滤杯。我们实验的思路是在保持所有其他冲煮变量不变(烘焙度、水温、流速等)的情况下评估滤杯形状对咖啡风味的影响。设计实验回答“哪种形状的滤杯更好?”你首先要回答这个问题:“二者有区别吗?”为了确定是否存在差异,我们首先使用了“辨别测试”,也称为“三角杯测”。在这个测试中,一名测试小组成员将得到三杯咖啡,其中两杯是相同的,另一杯是不同的。小组成员要找出不同的那杯咖啡。由于每个小组成员都有三分之一的机会仅凭运气就能猜对,所以我们需要33%以上的小组成员能正确地识别出那杯不同的咖啡。如果这个前提没有达成,那么就证明两个不同形状的滤杯没有任何实质的区别。我们招募了45名非专家小组成员来品尝在加州大学戴维斯咖啡中心感官实验室里滴滤好的咖啡。实验室分成小隔间将测试者隔离开,测试方式是盲测,室内设有红灯用来减少基于咖啡颜色深浅的预判偏差。在三角形测试中,我们使用了所谓的“2×2”阶乘设计,使用了两种形状的滤杯和两种不同的研磨度(中度和中细)。这是“析因设计”的一种方式(析因设计(factorial design)是实验设计的一种。指以多因素(两个或两个以上)为研究对象,探求各因素的主效应和因素间的交互效应)我们进行了六组不同的三角形杯测,测试所有可能的组合(滤杯形状+研磨度(表1))。另外单独一组测试是滤杯形状和烘焙度的组合(两种烘焙度:深,浅)。测试的重点是确定滤杯形状和研磨粗细的相互影响。实验中最具挑战性的一个问题是准备细节,因为三角杯测的后勤准备工作非常重要。例如,如果有两杯咖啡比第三杯咖啡温度高,那么小组测试成员只是在区别温差而不是味觉上的差别,所以我们必须制定出程序,在完全相同的温度下,提供不同的咖啡。同样,我们发现我们必须将“倒注水高度”规定好,因为我们的一些志愿者注水高度高于其他人,由此产生了咖啡表面泡沫的差异,测试者仅仅通过视觉观察就可以看出咖啡之间的不同之处。我们花了相当多的时间来研究这些细节,以确保实验的严谨性。计算结果我们的努力是值得的,因为我们获得了令人兴奋的(而且违反直觉的)结果,总结在表1中。关注第一行,我们看到,当比较锥形滤杯和平底扇形滤杯的形状时,都使用了中等研磨度,45名小组测试成员中有25人正确识别出了那杯不同的咖啡。(之前我们我们预计小组成员中有三分之一的人(15人)仅仅靠运气就能答对)。
—— 本文最先刊登在SCA网站 ——在一个挤满咖啡爱好者的房间里要想引发一场激烈的争论,最好的方法之一就是问一个简单的问题:滴滤咖啡用什么形状的滤杯最好?SCOTT FROST博士、JEAN-XAVIER GUINARD教授和WILLIAM D. RISTENPART教授分享了与SCA和Breville公司合作进行的一个研究项目的早期成果。滴滤咖啡都需要一个滤杯,要么是锥形要么是平底扇形。锥形滤杯粉丝们称锥形滤杯提高流过咖啡粉床的流量,增加萃取均匀度,相应地改善口味。令人困惑的是喜欢平底扇形滤杯的人会说平底扇形滤杯也有同样的好处。支持一种观点或另一种观点的证据往往涉及个人的口味。到目前为止,对此争论缺少的是科学数据。2017年,SCA要求加州大学戴维斯咖啡中心(University of California Davis Coffee Center)开展研究,旨在更新传统滴滤咖啡萃取控制表( brewing control chart)。这项研究正在进行中(取得了令人兴奋的初步结果)。我们也决定尝试着解决有关锥形滤杯和平底滤杯的争论。我们很幸运地与Breville Corporation合作,Breville Corporation滴滤机其特点是可以轻松地更换锥形滤杯和平底扇形滤杯。我们实验的思路是在保持所有其他冲煮变量不变(烘焙度、水温、流速等)的情况下评估滤杯形状对咖啡风味的影响。设计实验回答“哪种形状的滤杯更好?”你首先要回答这个问题:“二者有区别吗?”为了确定是否存在差异,我们首先使用了“辨别测试”,也称为“三角杯测”。在这个测试中,一名测试小组成员将得到三杯咖啡,其中两杯是相同的,另一杯是不同的。小组成员要找出不同的那杯咖啡。由于每个小组成员都有三分之一的机会仅凭运气就能猜对,所以我们需要33%以上的小组成员能正确地识别出那杯不同的咖啡。如果这个前提没有达成,那么就证明两个不同形状的滤杯没有任何实质的区别。我们招募了45名非专家小组成员来品尝在加州大学戴维斯咖啡中心感官实验室里滴滤好的咖啡。实验室分成小隔间将测试者隔离开,测试方式是盲测,室内设有红灯用来减少基于咖啡颜色深浅的预判偏差。在三角形测试中,我们使用了所谓的“2×2”阶乘设计,使用了两种形状的滤杯和两种不同的研磨度(中度和中细)。这是“析因设计”的一种方式(析因设计(factorial design)是实验设计的一种。指以多因素(两个或两个以上)为研究对象,探求各因素的主效应和因素间的交互效应)我们进行了六组不同的三角形杯测,测试所有可能的组合(滤杯形状+研磨度(表1))。另外单独一组测试是滤杯形状和烘焙度的组合(两种烘焙度:深,浅)。测试的重点是确定滤杯形状和研磨粗细的相互影响。实验中最具挑战性的一个问题是准备细节,因为三角杯测的后勤准备工作非常重要。例如,如果有两杯咖啡比第三杯咖啡温度高,那么小组测试成员只是在区别温差而不是味觉上的差别,所以我们必须制定出程序,在完全相同的温度下,提供不同的咖啡。同样,我们发现我们必须将“倒注水高度”规定好,因为我们的一些志愿者注水高度高于其他人,由此产生了咖啡表面泡沫的差异,测试者仅仅通过视觉观察就可以看出咖啡之间的不同之处。我们花了相当多的时间来研究这些细节,以确保实验的严谨性。计算结果我们的努力是值得的,因为我们获得了令人兴奋的(而且违反直觉的)结果,总结在表1中。关注第一行,我们看到,当比较锥形滤杯和平底扇形滤杯的形状时,都使用了中等研磨度,45名小组测试成员中有25人正确识别出了那杯不同的咖啡。(之前我们我们预计小组成员中有三分之一的人(15人)仅仅靠运气就能答对)。 表1现在的问题重点是:这25人是不是靠运气猜对的。为了回答这个问题,我们使用了所谓的“二项概率分布”。二项概率分布伯努利试验设试验E只可能有两种结果:“A”和“非A”,则称试验E为伯努利试验例如抛硬币其结果可有两个若“A”表示得到正面则“非A”表示得到反面(如前文所述,在本次实验中,“硬币”正面朝上的概率为33%,即45人中有15人凭运气就可以猜出哪杯是不同的咖啡)将E独立的重复地进行n次,则称这一串重复的独立试验为n重伯努利试验二项分布亦称“伯努利分布”.设将一伯努利试验重复了n次,在这n次试验中成功次数x,x为随机变量,称为二次随机变量,其分布称为二项分布.假设每次成功的概率为p,则在n次试验中成功k次的概率为 p(x=k)=Cnk Pk(1-p)n-k (0≤k≤n)利用这个分布,我们能够计算出25位小组成员仅仅靠随机运气得到正确答案的概率或“p值”。这里的p值是0.004,这意味着如果我们重复实验1000次,25个小组成员在这1000个实验中只有4人可以正确找到那杯不同的咖啡。这个分布概率推断这不太可能!换句话说,这25人不是侥幸地找到那杯不同的咖啡,咖啡风味(从统计学角度看)上有显著的可察觉的差异。我们观察到一个类似的结果,对于使用锥形滤杯和平底扇形滤杯冲煮更细研磨度的咖啡,测试小组成员中有23人可以找出那杯不同的咖啡(p值为0.024)。因此,对于所有认为滤杯形状会影响咖啡口感的咖啡爱好者来说,我们的数据表明他们的这个论点是绝对成立的。然而,令人惊讶的是三角杯测也显示,这些非专家小组测试成员无法区分研磨度粗细(对风味影响)的差异。表1的第3行和第4行显示了同样形状滤杯但不同研磨度的三角杯测结果。使用平底扇形滤杯时,只有18名小组成员找出了不同的咖啡;而在使用锥形滤杯时也才有15人识别出不同的咖啡。这个概率非常低。我们的“中等研磨”的粒度为1065微米,而我们的“中细研磨”的粒度为799微米,大小相差25%。对于那些认为精确控制咖啡研磨大小的极端重要的咖啡爱好者来说,事实证明——至少对于滴滤咖啡来说——普通人分辨不出两者之间的区别(至少需要超过这个研磨度大小的范围)。上面描述的三角杯测显示出了明显的区别,但是它们没有说明区别是什么。为了解决这个问题,我们接下来进行了一系列详细的“感官描述”实验(sensory descriptive experiments)。在这种类型的测试中,我们请训练有素的专家小组成员评估各种味道属性的强度,如“烟熏味”、“柑橘味”、“苦味”等。我们也邀请了表现最好的非专家小组成员(那些在三角杯测中表现最好的人)加入我们的专家小组。我们对他们进行了感官校正。然后,我们让他们评估来自8种不同设计组合(“2×2×2”阶乘设计:2种滤杯形状,2种研磨度,2种烘焙度)的26种不同的风味属性(flavor attributes)。专家小组盲测了了每种组合,并提供了26种风味属性的先后排名。12名专家小组成员,每个人品测26个风味属性,8个不同的组合,重复3次,得到12×26×8×3 = 7,488个个体数据点。不用说采集这么大的数据集很有挑战性。图2中提供了一个图像摘要,展示了所谓的“主成分分析”。这是一种先进的统计技术,用于获取大量数据集,并将其缩减为最有意义的“主成分”,以帮助确定小组中哪些人的感官最不相似或最相似。
表1现在的问题重点是:这25人是不是靠运气猜对的。为了回答这个问题,我们使用了所谓的“二项概率分布”。二项概率分布伯努利试验设试验E只可能有两种结果:“A”和“非A”,则称试验E为伯努利试验例如抛硬币其结果可有两个若“A”表示得到正面则“非A”表示得到反面(如前文所述,在本次实验中,“硬币”正面朝上的概率为33%,即45人中有15人凭运气就可以猜出哪杯是不同的咖啡)将E独立的重复地进行n次,则称这一串重复的独立试验为n重伯努利试验二项分布亦称“伯努利分布”.设将一伯努利试验重复了n次,在这n次试验中成功次数x,x为随机变量,称为二次随机变量,其分布称为二项分布.假设每次成功的概率为p,则在n次试验中成功k次的概率为 p(x=k)=Cnk Pk(1-p)n-k (0≤k≤n)利用这个分布,我们能够计算出25位小组成员仅仅靠随机运气得到正确答案的概率或“p值”。这里的p值是0.004,这意味着如果我们重复实验1000次,25个小组成员在这1000个实验中只有4人可以正确找到那杯不同的咖啡。这个分布概率推断这不太可能!换句话说,这25人不是侥幸地找到那杯不同的咖啡,咖啡风味(从统计学角度看)上有显著的可察觉的差异。我们观察到一个类似的结果,对于使用锥形滤杯和平底扇形滤杯冲煮更细研磨度的咖啡,测试小组成员中有23人可以找出那杯不同的咖啡(p值为0.024)。因此,对于所有认为滤杯形状会影响咖啡口感的咖啡爱好者来说,我们的数据表明他们的这个论点是绝对成立的。然而,令人惊讶的是三角杯测也显示,这些非专家小组测试成员无法区分研磨度粗细(对风味影响)的差异。表1的第3行和第4行显示了同样形状滤杯但不同研磨度的三角杯测结果。使用平底扇形滤杯时,只有18名小组成员找出了不同的咖啡;而在使用锥形滤杯时也才有15人识别出不同的咖啡。这个概率非常低。我们的“中等研磨”的粒度为1065微米,而我们的“中细研磨”的粒度为799微米,大小相差25%。对于那些认为精确控制咖啡研磨大小的极端重要的咖啡爱好者来说,事实证明——至少对于滴滤咖啡来说——普通人分辨不出两者之间的区别(至少需要超过这个研磨度大小的范围)。上面描述的三角杯测显示出了明显的区别,但是它们没有说明区别是什么。为了解决这个问题,我们接下来进行了一系列详细的“感官描述”实验(sensory descriptive experiments)。在这种类型的测试中,我们请训练有素的专家小组成员评估各种味道属性的强度,如“烟熏味”、“柑橘味”、“苦味”等。我们也邀请了表现最好的非专家小组成员(那些在三角杯测中表现最好的人)加入我们的专家小组。我们对他们进行了感官校正。然后,我们让他们评估来自8种不同设计组合(“2×2×2”阶乘设计:2种滤杯形状,2种研磨度,2种烘焙度)的26种不同的风味属性(flavor attributes)。专家小组盲测了了每种组合,并提供了26种风味属性的先后排名。12名专家小组成员,每个人品测26个风味属性,8个不同的组合,重复3次,得到12×26×8×3 = 7,488个个体数据点。不用说采集这么大的数据集很有挑战性。图2中提供了一个图像摘要,展示了所谓的“主成分分析”。这是一种先进的统计技术,用于获取大量数据集,并将其缩减为最有意义的“主成分”,以帮助确定小组中哪些人的感官最不相似或最相似。 图2图2为主成分分析图,将最相似的统计结果分组在一起。从这里,我们可以看出最大的区别是浅烘焙和深烘焙之间的区别,而且滤杯的形状也对差异发生了实质作用。
图2图2为主成分分析图,将最相似的统计结果分组在一起。从这里,我们可以看出最大的区别是浅烘焙和深烘焙之间的区别,而且滤杯的形状也对差异发生了实质作用。 图3:概述了每个分组的风味属性。锥形滤杯的浅烘焙咖啡带有酸感,柑橘和浆果的味道;风味描述中有葡萄干、干果和甜美的花香。从上图中可以得到一些有用的信息。首先,不出意料的是,浅烘焙和深烘焙之间存在着很大的风味差异。更有趣的是,我们发现对于给定的烘焙度(例如,左边的浅烘焙)滤杯形状也产生了有意义的差异。平底滤杯有更多的干果、甜感和花香,而锥形滤杯则有更多的柑橘、浆果和酸感。同样的,滤杯的形状也影响了深烘焙,平底滤杯产生了更明显的巧克力、可可和木质口味,而锥形滤杯则产生了更强烈的苦味。哪个形状的滤杯最好?这是一个关键点,让我们重申一下:使用完全相同的咖啡,相同的水,相同的温度,相同的流量,我们能够通过改变滤杯形状(以一种非常明显的,统计上显著的方式)改变咖啡的风味。在证明了存在差异以及差异是什么之后,最后一个问题是“为什么存在差异?”滤杯的形状会影响液体流过咖啡粉床的方式,从而改变分子从固体(咖啡颗粒)中被萃取及进入液体的“质量传递”过程。这个过程的基本细节是复杂的;加州大学戴维斯咖啡中心(UC Davis Coffee Center)正在积极深入地研究这一点。对于:“哪种形状的滤杯是“最好的”?答案应该是:最适合你的口味的冲煮方式就是“最好的”,这取决于每个人的决定。(这个结论结论似乎一万年前,所有的人都知道)不过,至少,下次有人开始讨论平底滤杯和锥形滤杯的优缺时,您可以使用本文中的数据来阐明这场争论。全文完
图3:概述了每个分组的风味属性。锥形滤杯的浅烘焙咖啡带有酸感,柑橘和浆果的味道;风味描述中有葡萄干、干果和甜美的花香。从上图中可以得到一些有用的信息。首先,不出意料的是,浅烘焙和深烘焙之间存在着很大的风味差异。更有趣的是,我们发现对于给定的烘焙度(例如,左边的浅烘焙)滤杯形状也产生了有意义的差异。平底滤杯有更多的干果、甜感和花香,而锥形滤杯则有更多的柑橘、浆果和酸感。同样的,滤杯的形状也影响了深烘焙,平底滤杯产生了更明显的巧克力、可可和木质口味,而锥形滤杯则产生了更强烈的苦味。哪个形状的滤杯最好?这是一个关键点,让我们重申一下:使用完全相同的咖啡,相同的水,相同的温度,相同的流量,我们能够通过改变滤杯形状(以一种非常明显的,统计上显著的方式)改变咖啡的风味。在证明了存在差异以及差异是什么之后,最后一个问题是“为什么存在差异?”滤杯的形状会影响液体流过咖啡粉床的方式,从而改变分子从固体(咖啡颗粒)中被萃取及进入液体的“质量传递”过程。这个过程的基本细节是复杂的;加州大学戴维斯咖啡中心(UC Davis Coffee Center)正在积极深入地研究这一点。对于:“哪种形状的滤杯是“最好的”?答案应该是:最适合你的口味的冲煮方式就是“最好的”,这取决于每个人的决定。(这个结论结论似乎一万年前,所有的人都知道)不过,至少,下次有人开始讨论平底滤杯和锥形滤杯的优缺时,您可以使用本文中的数据来阐明这场争论。全文完 看的懂的看不懂的,动动手指分享到朋友圈好东西,就是要分享!也欢迎留言!
看的懂的看不懂的,动动手指分享到朋友圈好东西,就是要分享!也欢迎留言! 手机浏览中华饮品届
手机浏览中华饮品届













