手机浏览中华饮品届
拉花的基础物理学原理液体表面存在张力，粘稠/密度大液体表面张力更大，倾倒奶泡的过程中，每单位时间内倾倒的奶泡都同时受到：1：重力2：浮力（阿基米德定律，见流体静力学）3：液体表面张力4：同时流动的液体受伯努力定律（见流体动力学）影响在这四者共同作用下，后续倒入的奶泡可以在原有的混合物（esp+先倒入的奶泡）的表面形成一定的形状并在一定时间内保持不变的结果，即我们所理解的拉花（表面成型）。关键词：重力，液体表面张力（区别于“张力”），浮力，流体力学（流体静力学和流体动力学，会分开讲解。）。百度一下以上名词可以搜出无数公式和定义，但受限于物理知识的专业性，大部分难以读懂，这里只做关系到拉花的部分通俗讲解，希望给大家（特别是咖啡师们）一点即通的效果，但涉及知识面较多，需要一定逻辑性，感谢耐心阅读的读者。
另，物理的严谨性，很多情况下公式以及原理只适用于理想状态，字字追究，较真者不喜勿阅。比如1：液体表面张力的多种测试公式在液体微观均匀（例如溶剂）的情况下适用，但咖啡制作的过程无法将咖啡制作成一杯“绝对均匀”的“溶剂”（因为奶泡和esp爆裂及挥发的不稳定性，或是奶泡气泡以及咖啡细粉微粒无法绝对均匀，等等），所以，只能是在宏观下（例如认定奶泡无论粗细，但气泡大小是均匀的），或是相对情况下的比较。2：阿基米德定律是流体静力学的一个分支，只在静止下成立，有明显流动的液体不成立，例如鱼的密度比水小，所以死鱼会浮在水面上，但鱼可以通过摆动鱼鳍，让水流动，使身体在水下保持一个相对静止的状态，所以此时阿基米德定律便不成立，所以很多时候，我们需要微观的去研究一个点，在某一时刻认定当下的状态（例如，融合结束拉花前，认定液体在那一刻处于静止状态。）来判定，从而展开分析研究。
重力(G)：计算公式是：G=mg，g为比例系球，m为重量，而，m=ρv，v为体积，ρ为密度。所以，G=ρvg。再所以，咖啡制作中，不难理解，奶泡越“粗/厚”，空气占比越大，ρ越小，等体积下质量越小，受到的重力也越小。在其他力（浮力，液体表面张力）相等的情况下（理想单一变量），相对静止情况下忽略伯努力定律，并且假定操作完全相同。那么得出拉花结论：越“粗/厚”的奶泡，越容易浮在Esp表面。所以，如果一个初学者想倒一个大白心，一杯厚奶泡很容易实现。而物理结论是：静态下，越厚的奶泡，等体积下，受到的G越小。亦或者，动态下，等时间下，倾倒的奶泡（流速）越多，G越大。（*星标1）。
液体表面张力（*f2）：（节选自《高等物理》）使液体表面积缩小的力，称为液体表面张力。它产生的原因是 液体跟气体接触的表面存在一个薄层，叫做表面层，表面层里的分子比液体内部稀疏，分子间的距离比液体内部大一些，分子间的相互作用表现为引力。阿基米德定律：浸入静止流体中的物体受到一个浮力，其大小等于该物体所排开的流体重量，方向垂直向上并通过所排开流体的形心。
液体表面张力很容易理解，也很容易在日常生活中看见，比如树叶上的水珠，比如卡布奇诺鼓起的奶泡等等，
而它的大小受诸多因素影响，在咖啡中适用（相对）的，有两个因素：1：同样的液体，温度越高，表面张力越小。2：分子量（咖啡中可以理解为密度）越大的液体，表面张力越大。（*星标4）而表面张力会形成一个垂直于液面向外的力，所以在无重力影响的太空舱，水滴会成球形而不是水滴形。而在咖啡中，我们可以理解为，奶泡的表面，由于张力的存在，表面会有一个向上的力的存在。由于空气的存在浓缩咖啡的密度是大于奶泡的，所以静止状态下，由于浓缩+奶泡的混合物的密度ρ1>奶泡的密度ρ2，会产生一个浮力f1（*星标2），再加上表面张力f2的存在，此时，标注奶泡的重力为G1
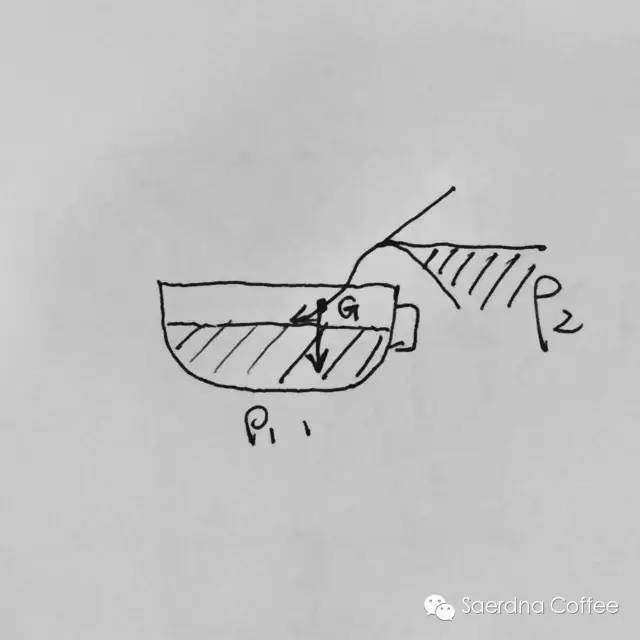则G1=f1+f2（*星标3）此时，奶泡则以一个相对稳定的状态，浮在咖啡（混合物）表面。（成型的基础原理）浮力（f1）：根据阿基米德原理，浸入静止流体中的物体受到一个浮力，其大小等于该物体所排开的流体重量，所以，倾倒入的奶泡收到的浮力是和倾倒入混合物中的奶泡所排开的混合物的体积所决定的。即f1=G=ρvg，所以，常常会看到拉花的纹路成“浮雕”状，则是由于冲量的存在，排开了一定体积的混合物，受到的浮力则满足星标3的等式，图案则成型。
等式在什么时候不成立（什么时候无法拉花？什么时候“拉花拉不出来”）？奶泡在拉花时为流动状态，会产生动量p=mv继而根据动量以及冲量的守恒公式f3t=mv得出，f3=mv/t[f3为单位奶泡接触液面时所产生的作用力，m为奶泡质量，流速越大，单位时间接触液面的奶泡质量越大，流速稳定时视为恒量（*星标5），t为接触时间，奶泡厚薄相同时时视t为恒量，v是奶泡接触液面的速度]
首先，请花几分钟时间详细阅读上文（冲量&动量），并尽可能理解。然后，运动状态下，液体表面受f1,f2,f3，G的影响，G+f3=f1+f2时候，倾倒的奶泡浮起，形成图案，G+f3>f1+f2时候，倾倒奶泡下沉，不能形成图案。
那，什么原因，让G+f3>f1+f2？根据公式，f3中，m，t都是恒量，则，v越大，f3越大。v由什么决定？奶泡的倾倒（下落）过程中，下落时间越长，由于重力加速度（是指一个物体受重力作用的情况下所具 有的加速度）的存在，v越大。什么情况下下落时间越长？奶泡的初始高度越高，下落时间便越长，v便越大，f3便越大，当G（重力）+f3（接触作用力）>f1（浮力）+f2（液面张力）时，拉花便不能形成。而G+f3<f1+f2的情况是不存在的。由于G的存在，奶泡只可能浮在液体表面，或是沉入液体以下，不可能向上运动。当然，为了满足G+f3=f1+f2，我们有很多种方法，减小G [ 减小单位时间流量（*见星标1）]，或是减小f3（降低注入高度），都可实现。亦或者增大f1（更高浓度的Esp）或者f2 [更低温度的混合物，可通过降低奶泡温度实现（*见星标4），或是更浓密的cream，比如罗豆，亦或者更新鲜的咖啡豆，也可以实现。] 来实现。
如果关于冲量及动量还没有理解，那么，我这里再举个例子：一个50g的小钢珠和一个5kg的铅球，同样在20cm 高度抛下，铅球可以把手砸伤但小钢珠不会，但如果下落高度只有2cm，一个女孩也可以稳稳接住铅球，再如果，如果是30米高处抛下小钢珠，也可以砸伤人甚至致死。 变量是，质量，高度，以及接触速度，接触时间，比如，我们通过一个缓冲的手势（增加接触时间），也可以轻易的接住20cm处抛下的铅球。生活中的例子也无处不在，例如原地跳起落下不会受伤，但3层楼落下基本可以摔死，但如果落在气垫上又可以避免受伤，再例如，一个很小质量的物体，如果以很高的速度接触你，会造成很大伤害，比如子弹，和高空落物。期望大家能理解上段原理，并对应到拉花操作中。
而提高注入，亦或者减小单位时间流量又会带来如下变量（改变G和f3）倾倒正视图解析（提高注入所带来的影响）：牛奶的下落是一个由粗变细的过程，原因是什么？伯努力定律：p+1/2ρv2+ρgh=C如果这个流体力学的纯公式很难看懂，那我们可以同通俗的以一句话大致概括：理想流体（理论无杂质，密度均匀），等高环境中，流体流速大，压力就小。随着下落高度的越来越大，速度越来越大，而流柱的压力越来越小，从长扁截面，会被空气逐渐挤压压成一个圆柱体截面（宽度变小），而随着下落高度到了一定极限，流柱内外压力差过大，流体最终被挤压为不规则形状。
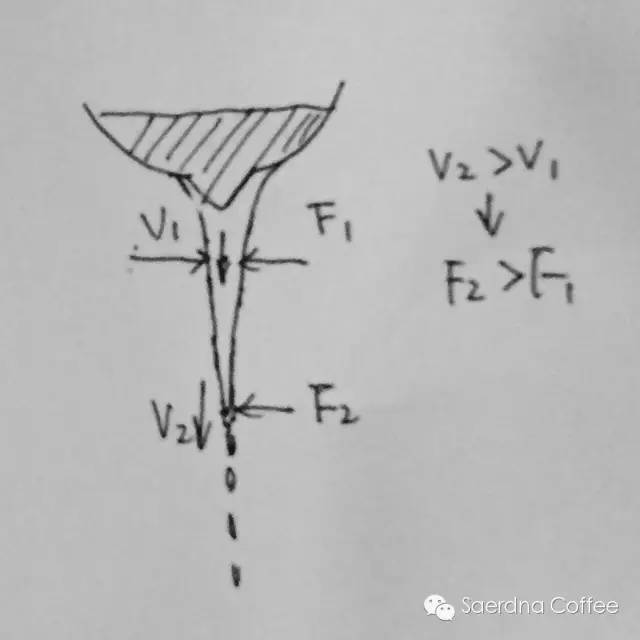而更小的截面面积会带来更大的正向压力，例如，用手掌按破一个气球很难，手指则容易些，用一根针则非常容易。而在拉花中的结论：下落高度（满足G+f3=f1+f2的情况下）决定初始色块大小，太高无法成型（过细的流量增加了正向压力，大于液面所带来的张力）惯例，如果伯努力定律没有理解，那么这里我举一些生活中的例子：例如不能靠火车太近，否则你和火车中快速流动的气体会让你被火车“吸”过去，而发生事故。还有，由于机翼的截面形状，飞机高速运动时，流过机翼上下面的气体流速不同，由于伯努力定律，上下面的压力也不同，当速度快到一定程度，机翼下面和上面的受力差大到一定程度，飞机就飞起来了。
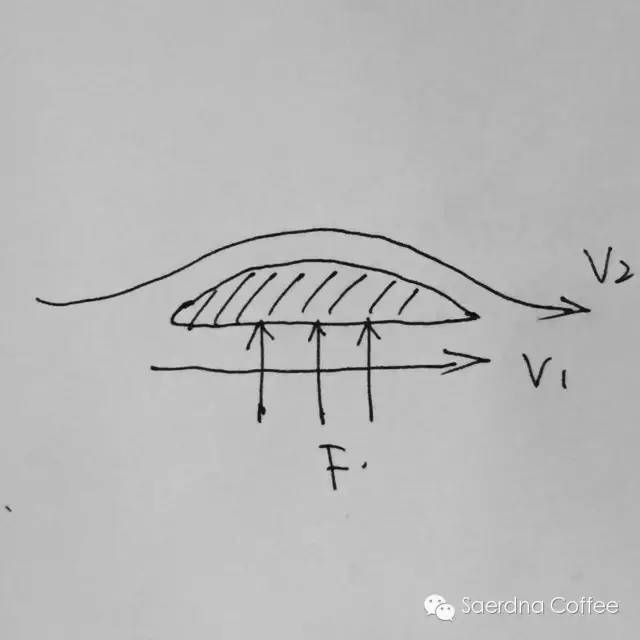这些都源于伯努力定律，经典的流体动力学在生活中的应用。刚才讲到奶泡下落，那么，详细如下。倾倒侧视图解析（改变流量所带来的影响）：奶泡的倒入是一个抛物线，而接触的液面始终是一个水平面。当由于力的分解原理，一个斜方向的力，可以按直角三角形，分解为水平和垂直两股力，接触液面的角度越小，分解出向前的力越多，向下的力越小，越容易成型，反之，越不易成型。
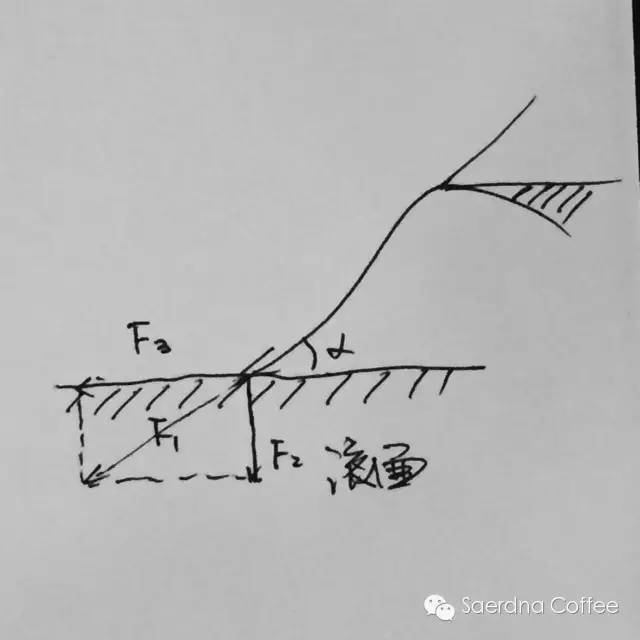如何减小这个角度？如图：同一高度下，流量越大，接触角度越小。同一流量下，高度越小，接触角度越小。
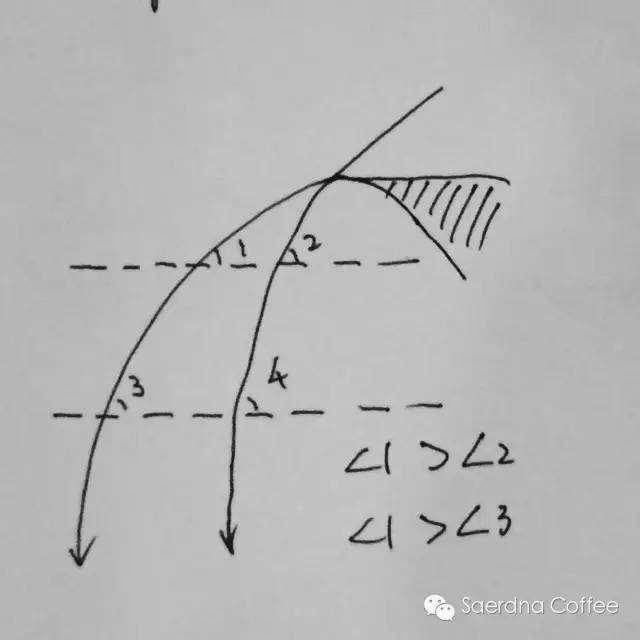所以，初学者拉不出花的时候，会疑惑，为什么你倒就有白颜色，而我倒就没有，排除奶泡和esp本身区别，无非于两种原因，流量太小，高度太大，或者两者兼有。增大流量很容易，如何降低高度？如图，奶缸尽可能靠近杯子的同时，你还要倾斜你的杯子，才能克服固有的液面到杯口的距离。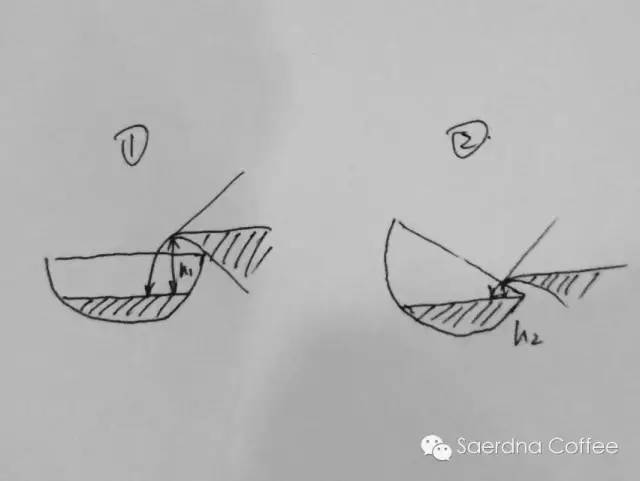
倾倒高度流量的共同影响解析：由于流柱存在着一定的宽度，如若注入高度过小，虽然可以满足G+f3=f1+f2公式（有图形出现），但在摆动中，成型轨迹依然有重叠（d1过小），即会造成，纹路心越向中间纹路越不明显，而rosetta的叶片最终越来越小，纹路最终消失，更不用提空心。
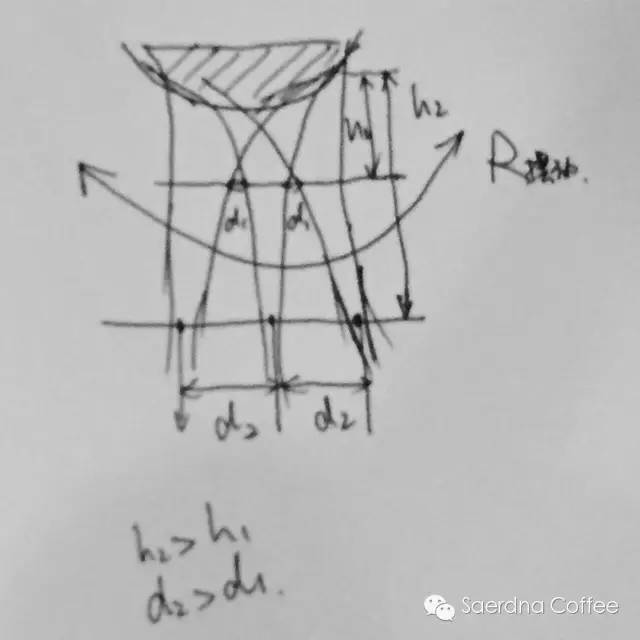问题的所在，更多的时候，并不是你的摆动手法有问题，而是因为，随着倾倒的奶泡越来越多，液面逐渐上升，注入高度逐渐缩短，流动轨迹逐渐重合。最终导致大块白色（亦或者越来越小的纹路幅度）的出现。解决方法？随着注入逐渐提高注入点，以维持摆动流动轨迹的空隙（d2）。如果你理解并掌握了这一点，传说中的“满杯纹路”，以及“空心叶”也并没有那么多传说了。并不仅仅涵盖这两个图，这些物理原理可以涵盖几乎所有拉花图案，剩下的无非是一些手法细微差别。当然，这是在esp及奶泡稳定，其他硬件条件统一的条件下，以上所有才成立，而关于奶泡打发，豆子的调整及萃取，奶缸杯具的挑选，及硬件设备的使用，每一变量都可以整理出一篇长篇“论文”，而此文也仅仅是我拉花课程框架其中一部分，仅供大家参考。培训师也可以在理解的基础上，把上文知识作为教学使用。又当然，理解是掌握的前提，没有理解只能是盲目练习，而若理解后没有练习，理解也并不等于掌握。其实公式很多地方可以查到，原理文案也可以百度百科，依稀记得大学毕业时独立完成了一篇叫“自动监测环境温度系统的搭建和使用”的毕业论文（很多自动控制专业的理工科毕业生都应该有印象。），而没有靠ctrl+c和ctrl+v，如果相比那篇接近8w字的理工科论文，拉花实在是太简单了。老话说，学好数理化，走遍天下都不怕。老话说，师者，传道授业解惑。老话还说，匠心独运，生财有道，匠人和商人本不冲突，做一行爱一行尊重一行，从业人自勉。
本文节选转载自“Saerdna Coffee”微信公众号（id：SaerdnaCoffee），为近两年前的一篇良心好文，分享给大家，也感谢Saerdna Coffee的主理人宝哥（徐晓平，下图左）和涛哥（李涛，下图右）对男神拉花赛的大力支持！
喜欢这篇文章的你，请分享给身边同样喜欢咖啡的伙伴，分享，让大家共同进步！
